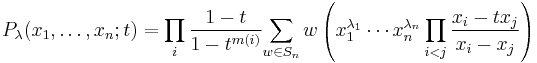Hall–Littlewood polynomials

In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter t and a partition λ. They are Schur functions when t is 0 and monomial symmetric functions when t is 1 and are special cases of Macdonald polynomials. They were first defined indirectly by Philip Hall using the Hall algebra, and later defined directly by Littlewood (1961).

Contents

Definition

The Hall–Littlewood polynomial P is defined by

P_\lambda(x_1,\ldots,x_n;t) = \prod_{i}\frac{1-t}{1-t^{m(i)}} {\sum_{w\in S_n}w\left(x_1^{\lambda_1}\cdots x_n^{\lambda_n}\prod_{i<j}\frac{x_i-tx_j}{x_i-x_j}\right)}

where λ is a partition of length at most n with elements λi, and m(i) elements equal to i, and Sn is the symmetric group of order n!.

See also

References

External links